We live in a three-dimensional world. Although we can conceive of three dimensions or less—the one-dimensional line and the two-dimensional surface—it is difficult for us to imagine dimensions higher than three. However, mathematicians conducting research into space claim to be able to “visualize” four-dimensional space. What exactly do we mean by the expression “research into space”?
A world of shadow created by light

Sometimes the true form of objects casting a shadow cannot be determined from the shape of the shadow itself.
Kumi Yamashita's “Profile (1994)” (Wood, Light, Cast Shadow/H150 cm x W300 cm x D8 cm)
The letters and numbers scattered on the wall, lit from the left, cast a silhouette of a man's face.
© Kumi Yamashita
We imagine the original form of an object from the shadow that is generated by light. From its shadow, we can imagine whether the actual form is, let's say, that of an adult or a child, is tall or short, or has long hair or short. However, although a shadow accurately reveals an object's profile, the object that generates the shadow is also part of a rich world that cannot be divined from the shadow itself. It is this type of ethereal unpredictability that the works of New York-based artist Kumi Yamashita project.
In his work The Republic, the Ancient Greek philosopher Plato expounded the “Allegory of the Cave” as follows.
“Imagine a cave, where prisoners who have been chained up since childhood sit facing a wall unable to turn their heads. They can only see shadows that are cast on the wall by a light from behind them. As they are unable to turn around and see what is behind them, they come to believe that the world of shadows is real. We probably do the same in the way that we perceive the world.”
Plato reasoned that—just like the prisoners turn around and see what it is that is creating the shadows— we will not be able to get closer to the truth unless we try to see the true nature of our surroundings.
At present, we perceive a rich world—it has color, people live in it, there is nature—that extends out into space. However, if we consider this concept of “light and shadow” from a wider perspective, this world itself could be the “shadow” cast by some other great world. Early mathematicians perceived this as a possibility.
What is dimension?
Dimension is a vital concept in our representation of space. Most people probably know that zero dimensions represent a point, one dimension a line, two dimensions a surface, and three dimensions a solid body. A shadow is a two-dimensional projection of a three-dimensional object generated by light.
Spatial dimension(s) can be defined as follows:
When a cross-section is zero dimensions—a point, the object is one-dimensional—a line.
When a cross-section is one dimension—a line, the object is two-dimensional—a plane.
When a cross-section is two dimensions—a plane, the object is three-dimensional—a solid.
In this instance, the expression “cross-section” denotes division of a space into two.
For example, we can imagine that if a “two-dimensional sphere” with zero thickness, such as a film like a soap bubble, is divided into two in three-dimensional space, the resulting cross-section will be a one-dimensional circle. However, it is a little difficult to imagine how if we can divide a solid “three-dimensional sphere,” like a ball, exactly into two in four-dimensional space, the resulting cross-section will be a “two-dimensional sphere.”
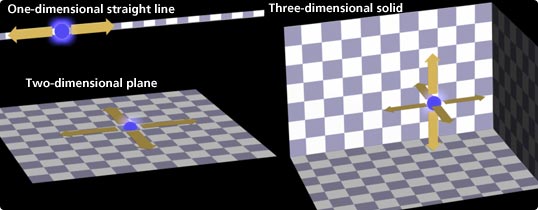
One dimension, two dimensions, and three dimensions can be represented using one coordinate (x), two coordinates (x, y), and three coordinates (x, y, z) respectively. In addition, they are respectively divided into two by zero dimensions—a point, one dimension—a line, or two dimensions—a plane.
It is not easy for us, living in our three-dimensional world, to imagine four-dimensional space in this way. If we hear the phrase “four dimensions,” we probably think of the three dimensions in which we live and “time” as one extra dimension.
For example, Einstein's theory of relativity specifies that nothing can travel faster than the speed of light, and it also mentions the slowing of time and the warping of space in the context of four dimensions, one of which is time. This article, however, describes the shape of space, as distinct from the real world.
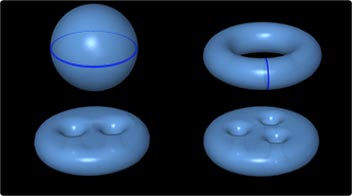
Two-dimensional spaces can be said to differ from one another when they have different numbers of holes.
Even within the same number of dimensions, there are several different types of space. In order to understand space, it is first necessary to classify it. First consider the case of two dimensions. In two dimensions, we can think, for example, of the surface of a hollow sphere or the surface of a hollow doughnut shaped object. These two spaces are of different types. To cut a long story short, two-dimensional space can be regarded as having a number of holes, such as 0, 1, or 2, and can be classified accordingly. Essentially, this hole count expresses the manner in which the surface is curved and is extremely important in classifying space.
Mathematics is the discipline that is used to tackle space in this manner—specifically, a branch of mathematics known as topology or “flexible geometry.” This field can handle infinite-order higher-dimensional realms that are difficult for us to conceive of. The higher-dimensional a space, the more difficult it would seem to classify and understand it. However, despite the great difficulty in understanding space of five or more dimensions, this has been achieved, and it is now realized that the most difficult challenge is posed by the so-called lower-dimensional spaces—those of three and four dimensions.
Major problems spanning generations
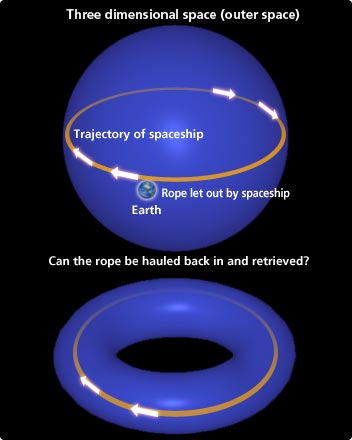
If a rope is let out in outer space and can be gathered back in to a single point by pulling on its two ends, the three-dimensional space is essentially a spherical surface. If the rope cannot be retrieved, the three-dimensional space is probably doughnut-shaped.
In mathematics, major problems are being tackled that have spanned the generations. In the year 2000, the Clay Mathematics Institute in the United States selected seven extremely difficult problems as the Millennium Prize Problems, with a cash prize of one million dollars to be awarded to anyone who could solve one of them. Although the awarding of cash prizes for solving problems in pure mathematics has its pros and cons, the Poincaré conjecture was selected as one of these hard problems.
The Poincaré conjecture is one of a class of problems relating to the classification of spaces. It poses the question of whether certain conditions hold at various different dimensions (that is, at zero dimensions, one dimension, two dimensions and so on). In 1960 the conjecture was solved for five or more dimensions, and then in 1981, albeit partially, for four dimensions. The three-dimensional case, however, remained unsolved to the last. The problem can be expressed in terms of the following simple analogy.
“When a rope is extended so that it goes right around a three-dimensional space and back to its point of origin, and if the rope can be retrieved by pulling its two ends simultaneously, this three-dimensional space is a spherical surface.”
In the case of a doughnut-shaped three-dimensional space, if a rope is extended and goes around the hole in the doughnut, the rope will snag when it is pulled and cannot be retrieved. Thus the question is, if it is possible to retrieve the rope, can the three-dimensional space be said to be in the form of a spherical surface? On the face of it, this appears to be a simple question. In fact, however, this problem of a correlation between the possibility of the rope being retrieved and the true shape of the space is extremely complex, and many mathematicians have dedicated their lives to its study.
At long last, however, this question was answered in the affirmative in 2002 by the brilliant Russian mathematician Perelman—his achievement sparking worldwide excitement.
The reason why the Poincaré conjecture was proved comparatively quickly for five dimensions and above, which are so-called higher-dimensional space, was that when the problem was tackled at higher dimensions, “surgery” was applied to the space, enabling it to be broken down into lower-dimensional space. The basic principle of this operation is known as the Whitney Trick, and is now fundamental to research in higher-dimensional topology.
In space of five dimensions and above, the Whitney Trick enables the removal of intersections between figures along a “disc.” Removal of this disc requires five-dimensional space, and when the disc itself intersects, there is insufficient space in three and four dimensions to remove this intersection. Hence, tackling this problem for three- and four-dimensional space came to be renowned for its difficulty.
On to the four-dimensional realm
A hypercube. Whereas a three-dimensional solid can be rotated about its three axes (x, y, and z), a four-dimensional solid can be rotated around its faces.
There is nothing more fascinating for mathematicians than the four-dimensional realm, because it is now realized that classification and understanding of four-dimensional space requires more profound theory than is needed for understanding higher-dimensional space. If the difficulties of four dimensions can be overcome, it should be possible to cope with unlimited numbers of dimensions in a unified fashion—which, for those of us in the three-dimensional world, is the stuff of our most grandiose dreams.
Mathematicians tackling this problem claim to be able to visualize the four-dimensional world in their heads. Unfortunately, without training it is impossible to visualize four-dimensional space, such as a four-dimensional hypercube created by moving a three-dimensional cube in an additional dimension direction.
“Two-dimensional space can be divided into several different types, according to the number of holes in them; however, there is no way to classify four-dimensional space, in a unified fashion. Shapes in four-dimensional space are gifts of nature and I feel like they form abruptly,” says Yukio Matsumoto, a professor at Gakushuin University and professor emeritus at the University of Tokyo who has been conducting four-dimensional research.
The 1980s was a great period of transition in four-dimensional research, as new techniques were introduced that were used in theoretical physics in the quest for a unified theory of the universe but in topology research for other dimensions. Many difficult problems were solved, and at the same time many other problems were presented. In this field, combining techniques both traditional and new, Professor Matsumoto made enormous progress.
It has been proved that it is impossible to completely classify all four-dimensional spaces. However, it would probably be possible to classify a limited range of four-dimensional spaces, reasoned Professor Matsumoto, and he imagined an evolving dynamically created space, with distinct two-dimensional surfaces known as “fibers” moving around on a two-dimensional surface, degenerating and regenerating from time to time. Following this line of thought, he proceeded to advance research into four-dimensional spaces that could be expressed as their trajectories.
Initially, there was a certain feeling that this represented a “toy four-dimensional theory,” says the professor. Subsequently, however, he realized that this constituted a fascinating area for researchers. Work on these spaces involved the use of new techniques, traditional topological research techniques, and techniques from disciplines such as algebraic geometry, thus representing a convergence of many different fields. Numerous researchers worldwide are joining in this research effort, and it is now developing into a major field.
Unlike the natural sciences, mathematical research does not deal with existing objects. Rather than being akin to fantasy, however, it represents the truth that underpins the effort to comprehend our world. In this fashion, mathematical research has been pursued continuously over the course of several thousand years. Understanding four-dimensional space leads us from the shadow world that Plato described to an understanding of the true world in all its glory.
Editorial contributor / Date of article posted
Yukio Matsumoto, Professor of Mathematics at Gakushuin University and University of Tokyo Professor Emeritus / August 2008

