Coverglass and spherical aberrations

Why is it necessary to have an objective designed to meet the standards of the coverglass holding your specimen?

For example, if you were to place a plate of glass over something, it wouldn't normally look very different other than appearing slightly closer. This is because the angle of a single ray of light coming off the object toward the observer's eye (also called numerical aperture in optical terms) is very small. In other words, if the numerical aperture is small a coverglass will not significantly effect how an object appears.

However, if the numerical aperture is large, such as in the case of an objective, then even a thin coverglass will negatively affect image quality. The main cause of this is something called 'spherical aberrations'.

As shown in Figure 1, when light rays L0-L3 bounce off the object P under a coverglass, they are each refracted within the coverglass before entering the objective. From the perspective of the objective, it will appear as though each of these light rays is coming from a different point. Even L0, with the smallest numerical aperture, appears as though it is coming from a point other than P. This is why objects with glass over them appear closer to the naked eye, with the depth of P0 equivalent to thickness (d) divided by refraction index (n). Deviations from this position become spherical aberrations.

When the numerical aperture is relatively small, such as light ray L1, the deviation from the P0 point is small. However, as the numerical aperture increases, spherical aberrations increase as well. This is why aberration design with coverglass spherical aberrations in mind is necessary when designing biological objectives with larger numerical apertures.

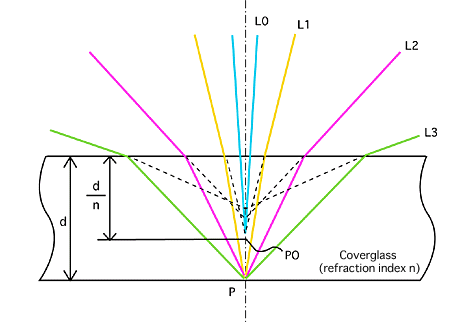
Figure 1. Refraction of light rays as they exit the coverglass.